Komputada Leksikono: La piramida ordigo

La piramida ordigo

Piramido estas duuma arbo en kiu nenia nodo havas ŝlosilon malplian ol tiuj de ĝiaj idoj. Evidente, piramido havas ĉe sia pinto (ĉe la radiko) la maksimuman datumanon de la arbo.

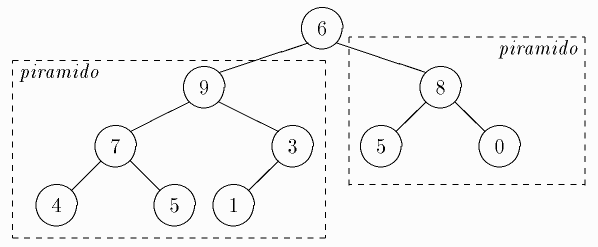
Eĉ se la du subarboj de duuma arbo estas piramidoj, la tuta arbo ne nepre estas piramido. Sed fari tian arbon piramido estas afero tre facila: sufiĉas viziti la vicon de la pli grandaj (pra)idoj, farante la necesajn permutojn, do, fari ne pli ol a paŝojn, se a estas la alto de la arbo (t.e. la longo de la plej longa vojo en la arbo). Tiel, por ekzempla arbo

bildo de piramida arbo
sufiĉas fari permutojn de 6 kun 9 kaj 7. Tiun procedon ni nomas rearanĝo de la arbo, aŭ mergo de ĝia radiko.

Estas sciate (vd duuma arbo), ke duuman arbon eblas prezenti per vektoro. Inverse, ĉe la piramida ordigo oni rigardas la ordigendan sekvencon v, apartenantan al (ekz-e)

TIPO vektoro = TABELO [1..n] EL entjera;

kiel prezenton de duuma arbo. La algoritmo de piramida ordigo havas du partojn, ĉiu el kiuj faras rearanĝojn.

Unue, ni faru la vektoron piramido — tiun stadion ni nomas piramidigo; due, tiun piramidon ni finordigos — la ordiga stadio.

Por realigi la piramidigon oni atentu, ke facilas apliki la rearanĝon al tiaj nodoj, kies idoj (se tiuj idoj ekzistas) jam estas piramidoj. Tian econ havas la vektoranoj kun la indicoj i EN [n DIV 2+1..n], ĉar ili estas senidaj. Do, oni piramidigas rekursie kaj «retropaŝe».

Post la piramidigo oni ricevas en v[1] la maksimuman datumanon. Permutante ĝin kun v[n] oni reduktas la problemon al la ordigo de la subvektoro v[1..n−1], kies du subarboj jam estas piramidoj; oni mergas v[1] en la subarbon, permutas v[1] kun v[n−1], ktp.

Piramida ordigo: Paskala programo

PROCEDURO piramidaOrdigo(VAR v:vektoro); 
   VAR i: entjera; x: reela; 
 
   PROCEDURO mergu(r, f: entjera); {-- radikon r en arbon v[r..f]} 
      VAR d, l: entjera; 
   STARTO 
      d := 2 * i; 
      l := d + 1; 
      SE d ≤ f TIAM STARTO    {-- trovu maks(v[r], v[l], v[d]): } 
         SE v[r] ≥ v[d] TIAM d := r; 
         SE l ≤ f TIAM SE v[l] > v[d] TIAM d := l; 
         SE r ≠ d TIAM STARTO          {-- permuto kaj mallevo: } 
            x := v[r]; v[r] := v[d]; v[d] := x; 
            mergu(d, f); 
         FINO 
      FINO 
   FINO {de "mergu"}; 
 
STARTO        { la korpo de piramidaOrdigo.  Unue la piramidigo: } 
   POR i := n DIV 2 SUBE 1 FARU mergu(i,n); 
   POR i := n SUBE 2 FARU STARTO        { ordigo de la piramido: } 
      x := v[i]; v[i] := v[1]; v[1] := x; 
      mergu(1, i - 1); 
   FINO 
 
FINO  { de "piramidaOrdigo" }