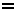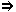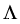Devenigi vorton de alia pli simpla:
la vorto „homaro“ deriviĝas de „homo“;
derivita vorto.
Devenigi vorton de alia pli simpla:
la vorto „homaro“ deriviĝas de „homo“;
derivita vorto.
 [1](fakula ĵargono)
(funkcion)
Kalkuli ties derivaĵon.
[1](fakula ĵargono)
(funkcion)
Kalkuli ties derivaĵon.