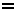tradukoj: de en es fr hu pl pt ru

divizor/o

divizoro

1.

[1](elementa aritmetiko) (de entjero a) Tia entjero b, ke a estas ĝia oblo: praktika avantaĝo de la dekduuma mezursistemo kuŝas en tio, ke 12 havas pli da oportunaj divizoroj: 2, 3, 4, 6, dum la kutima 10 havas nur 2 kaj 5 (sen kalkuli la neproprajn divizorojn 1 kaj memo). alikvoto.

2.

[2] (de elemento a en ringo aŭ multiplike signata monoido) Tia elemento b, ke por iu q, a = b.q (maldekstra divizoro) aŭ a = q.b (dekstra divizoro): la reela polinomo X²+1 ne akceptas unuagradajn reelajn divizorojn; la divizoroj de la unuo estas la inversigeblaj elementoj.

divizori

Esti divizoro: la fakton, ke b divizoras en a, oni simbole skribas b|a; 2 divizoras en ĉiu para entjero (aŭ „ĉiun paran entjeron“); komuna divizoro de pluraj entjeroj estas entjero, kiu divizoras ĉiun el ili.
Rim.: Laŭ sia senco la verbo estas netransitiva (en la ĉi-supra ekzemplo akuzativo anstataŭas prepozicion), tial oni teorie ne povus diri „divizorata“ aŭ „divizorebla“ (anstataŭ ĉi-lastan oni diru „divizorhava“ aŭ „dividebla“). La verbo „dividi“ estas teorie uzebla nur en frazoj de la tipo mi dividas a per b, sed la formo „dividanto“ jam sugestas, ke eblus diri b dividas a, se forgesi pri la homa plenumanto de la operacio. El tio sekvas, ke anstataŭ „divizori“ oni povus diri same bone „dividi ekzakte“, „dividi senreste“ aŭ eventuale nur „dividi“, kiel faras multaj naciaj lingvoj kaj ankaŭ [4].

divizorebla

(evitinde) dividebla.

divizorhava

(p.p. elemento en ringo) Tia, ke ekzistas propra divizoro de ĝi: por ke entjero estu divizorhava, sufiĉas, ke ĝi ne estu primo; divizorhava divizoro.
Rim.: Bricard [6] ĉi-sence uzas „komponita“.

nedivizoro

Elemento, kiu ne estas divizoro. alikvanto.

nuldivizoro

Tia nenula elemento p en ringo, ke por nenula elemento q veras, ke p×q aŭ q×p egalas al nulo: ĉiu kvadrategala bildigo p de la grupo (E,+) al si mem, egala nek al la nulo nek al la idento, estas nuldivizoro kadre de (E^E,+,◦), ĉar p◦(id_E-p) = 0. integra.

propra divizoro

(de elemento a en ringo) Tia divizoro, ke ĝi estas nek inversigebla, nek dividebla per a: propraj divizoroj de natura entjero estas ĉiuj ĝiaj divizoroj krom ĝi kaj 1; primo ne havas proprajn divizorojn.
Rim.: Ni ne trovis fonton por tiu termino kaj malgraŭ la ŝajno de internacieco ne konsideras ĝin senmanka, ĉar ĝi ne akordas kun la nefaka senco de la adjektivo „propra“ (apartenanta ekskluzive al iu). Tamen pro influo de naciaj lingvoj oni foje uzas „propra“ kun senco simila al „pura“, „vera“, ekz-e en la esprimo „proprasence“.

plej granda komuna divizoro (PGKD)

(de pluraj entjeroj) la plej granda komuna divizoro de 24 kaj 30 estas 6.

    Ŝajnas al mi, ke la senco "esti ~o de" ne tute malebligas,
    ke oni konsideru la verbon transitiva. Ja la ekz-oj de la tipo
    "2 ~as en la paraj nombroj" ne aspektas tre nature kaj transitiva
    verbo estus oportuna por traduki el la nacilingvoj, kiuj ĉisence
    uzas "dividi" metafore.
    [MB]