tradukoj: be de en fr hu nl pl ru

¹simetri/o

simetrio

1.

Harmonio rezultanta el proporcieco kaj regula aranĝo de partoj: simetrio estas bazo de arkitekturo, same kiel ritmo estas bazo de poezio aŭ muziko.

2.

Simetrieco: simetrio de la homa korpo..

3.

[1]

a)

(en vektora spaco) Homomorfia involucio: se U estas la aro de ĉiuj vektoroj senŝanĝaj per la simetrio f, kaj V estas la aro de ĉiuj vektoroj ŝanĝitaj al sia kontraŭegalo per f, tiam oni diras, ke f estas simetrio kun direkto V rilate al U. 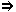vektora simetrio.

b)

(en afina spaco) Afina involucio: la homomorfio asociita al tia simetrio estas mem vektora simetrio. 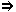oblikva simetrio.

c)

(en eŭklida afina spaco) Tia bildigo de la spaco al ĝi mem, ke ĉiuj strekoj kunligantaj punkton kaj ĝian bildon havas jenan econ: ilia mezo estas konstanta punkto (centra simetrio), aŭ ili estas ortaj en sia mezo al konstanta rekto (aksa simetrio) aŭ konstanta ebeno (ebena simetrio). 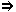orta simetrio;simetriakso, simetricentro, simetriebeno.

Rim.: Ial tiaj matematikaj sencoj aperas nek en [2], nek en [3], kiuj atribuas similajn al „reflekto“. Ja tiu termino en iuj naciaj lingvoj estas ofta sinonimo por „ebena simetrio“, sed ne ŝajnas konsilinde tute evakui la terminon „simetrio“. Ni do preferis sekvi [4].

simetria

1.

Havanta simetrion, aranĝita kun simetrio: la tuta aspekto de la sanktejo estas simetria^Z; iom tro simetria parolado; vazoj simetrie aranĝitaj.

2.

a)

[5] (p.p. geometria figuro) Tia, ke simetrio lasas ĝin senŝanĝa; alidire: per iu simetrio, la bildo de ajna punkto de ĝi apartenas al ĝi: sfero estas simetria rilate al sia centro kaj al ĉiu rekto aŭ ebeno enhavanta ĝian centron; elipso estas simetria rilate al siaj fokusa kaj nefokusa aksoj.

b)

[6] (p.p. (n,p)-matrico) Tia, ke ĉiu ĝia elemento kun indico (i,j) egalas al tiu kun indico (j,i): simetria matrico egalas al sia transponaĵo.

c)

[7] (p.p. interna rilato R) Tia, ke ĝi egalas al sia inverso R^-1: la idento-rilato estas simetria; R estas simetria, se kaj nur se de la fakto, ke xRy, sekvas, ke yRx; simetrieco estas nepra eco de ekvivalento-rilato.

d)

[8] (p.p. bildigo de Eⁿ al F, kun n ≥ 2) Tia, ke ĝi ĵetas ĉiujn opojn kun permutitaj termoj al la sama bildo: se n = 2 kaj f estas simetria, f(x,y) = f(y,x) por ĉiu ajn x, y.

e)

simetria diferenco.

malsimetria

(p.p. interna rilato R) Tia, ke la komunaĵo inter ĝi kaj ĝia inverso estas subaro de la idento-rilato; simb. R∩R^-1⊂id_E: se R estas malsimetria, de la fakto, ke xRy kaj yRx, sekvas, ke x = y.
Rim.: Pri la sencevoluo de tiu termino vd rimarkon sub antisimetria.

simetrieco

Eco de io simetria: la simetrieco de vizaĝo; se solido posedas aksan simetriecon, ĝi ne nepre estas rotacia.

oblikva simetrio

simetrio ^3.b.

orta simetrio

simetrio ^3.c.

vektora simetrio

simetrio ^3.a.