tradukoj:
de en es fr hu pl pt ru
konverĝ/i
Z
konverĝi
(ntr)
- 1.
- (p.p. linioj, direktoj, radioj)
Celi al sama punkto, kunveni:
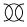 la sunaj radioj, trapasinte konveksan lenson,
konverĝas al ĝia fokuso [1].
la sunaj radioj, trapasinte konveksan lenson,
konverĝas al ĝia fokuso [1].
- 2.
 (fakula ĵargono en geometrio)
(p.p. linioj)
Havi komunan punkton:
ĉiuj naskantoj de
konuso konverĝas
(intersekciĝas) ĉe ĝia
vertico.
(fakula ĵargono en geometrio)
(p.p. linioj)
Havi komunan punkton:
ĉiuj naskantoj de
konuso konverĝas
(intersekciĝas) ĉe ĝia
vertico.
Rim.:
Ekzistas ankaŭ „kunkuri“, samsenca, kiel atestas
[2].
- 3.
 (elementa analitiko)
Senfina vico x1,
x2,...
konverĝas al p se por ajna pozitiva reelo
c ekzistas tia numero n, ke
|p-xi| < c
por ĉiu i > n.
(elementa analitiko)
Senfina vico x1,
x2,...
konverĝas al p se por ajna pozitiva reelo
c ekzistas tia numero n, ke
|p-xi| < c
por ĉiu i > n.
Rim.:
La nocion oni ĝeneraligas por funkcioj kaj serioj.
Tia p estas nomata limeso.
- 4.
 [3]
(p.p. vico aŭ
filtrilo super
topologia spaco)
Esti konverĝa 2:
laŭdifine ĉiuj koŝiaj vicoj konverĝas
en kompleta spaco.
[3]
(p.p. vico aŭ
filtrilo super
topologia spaco)
Esti konverĝa 2:
laŭdifine ĉiuj koŝiaj vicoj konverĝas
en kompleta spaco.
Rim.:
Kvankam la verbo enhavas ideon pri ago, ĝia matematika
uzo simple parolas pri eco de la koncerna vico. Oni diras
sendistinge „konverĝi“ aŭ „esti
konverĝ(ant)a“.
 diverĝi.
diverĝi.
konverĝa
- 1.
- (ĝenerale)
Konverĝanta.
- 2.

- a)
- [4]
(p.p. vico
(xn) en
topologia spaco)
Tia, ke ĉiuj ĝiaj termoj (krom finia nombro da ili)
apartenas
al ĉirkaŭaĵo
de iu punkto (ĝia
limeso), kiel ajn oni
elektas la
ĉirkaŭaĵon:
konverĝa serio (kies
vico de partaj sumoj konverĝas);
en metrika spaco, la
distanco inter termo xn
de konverĝa vico kaj ĝia limeso estas arbitre malgranda,
se n estas sufiĉe granda;
se vico akceptas adheran
punkton,
ekzistas konverĝa subvico de ĝi.
- b)
-
(p.p. filtrilo super
topologia spaco,
al iu punkto)
Pli fajna ol
la filtrilo de ĉirkaŭaĵoj de tiu punkto.
konverĝigi
-
Igi konverĝa:
 konverĝiga lenso
[5].
konverĝiga lenso
[5].
malkonverĝi

-
Ne konverĝi,
ne esti konverĝa.
 diverĝi.
diverĝi.
malkonverĝa, nekonverĝa
-
Ne konverĝanta:
 nekonverĝa serio
[6].
nekonverĝa serio
[6].
 diverĝa.
diverĝa.
absolute konverĝa
 [7]
[7]
-
(p.p. reela aŭ kompleksa
vico)
Tia, ke konverĝas la responda vico
de
absolutaj valoroj (aŭ
moduloj) de ĝiaj termoj:
ĉiu absolute konverĝa vico estas ankaŭ konverĝa,
sed la malo ne veras;
absolute konverĝa serio (kies responda serio de absolutaj
valoroj
konverĝas);
absolute konverĝa serio de funkcioj (absolute konverĝa por
ĉiu
valoro de la argumento).
konverĝa en distribuo

-
(p.p. vico
de hazardaj variabloj,
al limeso X)
Tia, ke la vico de iliaj
distribuaj funkcioj estas
simple konverĝa al la
distribua funkcio de X:
konverĝo en probablo implicas konverĝo en distribuo, sed ne
inverse.
konverĝa en mezuro
 [8]
[8]
-
(p.p. vico de funkcioj
(fn) de
mezurhava spaco
al metrika spaco,
al limeso f)
Tia, ke por ajna reelo ε la mezuro de la aro de
tiaj
x, ke la distanco de
fn(x)
al f(x) superas ε,
strebas al nulo, kiam n strebas al nefinio.
konverĝa en probablo
 [9]
[9]
-
(p.p. vico
de hazardaj variabloj,
al limeso X)
Konverĝa en
mezuro al X rilate al la
probablo.
malforte konverĝa
 [10]
[10]
-
(p.p. vico super
topologia
vektora spaco)
Konverĝa rilate al la
malforta topologio.
norme konverĝa

-
(p.p. vico super
normohava spaco)
Tia, ke konverĝas la responda vico
de
la normoj de ĝiaj termoj:
norme konverĝa serio (kies responda serio de normoj
konverĝas);
en kompleta spaco
ĉiu norme konverĝa vico estas ankaŭ konverĝa.
preskaŭ certe konverĝa

-
(p.p. vico
de hazardaj variabloj
(Xn), al limeso X)
Tia, ke la probablo de la aro de ĉiuj ω,
por kiuj la vico (Xn(ω))
ne konverĝas al X(ω), estas nula:
konverĝo preskaŭ certa implicas konverĝo en probablo.
simple konverĝa

-
(p.p. vico de funkcioj
(fn))
Tia, ke por ajna x la vico
(fn(x))
konverĝas al iu limeso
f(x):
simple konverĝi (esti simple konverĝa).
 topologio de
simpla konverĝo.
topologio de
simpla konverĝo.
unuforme konverĝa
 [11]
[11]
-
(p.p. vico de funkcioj
(fn) al
metrika spaco)
Tia, ke por iu funkcio f (ĝia
limeso)
veras, ke la supremo de la distancoj inter
fn(x)
kaj f(x)
konverĝas al nulo:
ĉiu unuforme konverĝa vico estas ankaŭ simple
konverĝa,
sed la malo ne veras;
unuforme konverĝi (esti unuforme konverĝa);
unuforme konverĝa serio (kies
vico de partaj sumoj unuforme konverĝas).
 topologio de
unuforma konverĝo.
topologio de
unuforma konverĝo.
Rim.:
En [12] troveblas
„konverĝegi“ anstataŭ „unuforme konverĝi“.
tradukoj
anglaj
~i 2.:
converge, be concurrent;
~i:
converge;
~a 2.:
convergent;
mal~i:
diverge;
mal~a, ne~a:
divergent;
absolute ~a:
absolutely convergent;
~a en distribuo:
convergent in distribution;
~a en mezuro:
convergent in
measure;
~a en probablo:
convergent in probability;
malforte ~a:
weakly convergent;
norme ~a:
normally convergent;
preskaŭ certe ~a:
almost
surely convergent, convergent
with probability one;
simple ~a:
simply convergent, pointwise convergent;
unuforme ~a:
uniformly convergent.
francaj
~i 2.:
converger, concourir;
~i:
converger;
~a:
convergent;
mal~i:
diverger;
mal~a, ne~a:
divergent;
absolute ~a:
absolument convergent;
~a en distribuo:
(suite de variables aléatoires)
convergente en loi;
~a en mezuro:
(suite de fonctions) convergente en
mesure;
~a en probablo:
(suite de variables aléatoires)
convergente en probabilité;
malforte ~a:
faiblement convergent;
norme ~a:
normalement convergent;
preskaŭ certe ~a:
convergeant presque sûrement;
simple ~a:
(suite de fonctions) simplement
convergente;
unuforme ~a:
(suite de fonctions)
uniformément convergente.
~iga:
(lentille) convergente.
germanaj
~i 2.:
durch denselben Punkt gehen;
~i 4.:
konvergieren;
~a 2.:
konvergent;
mal~i:
divergieren;
mal~a, ne~a:
divergent;
absolute ~a:
absolut konvergent;
~a en distribuo:
konvergent in Verteilung;
~a en mezuro:
konvergent dem
Maße nach;
~a en probablo:
konvergent in der Wahrscheinlichkeit;
malforte ~a:
schwach konvergent;
norme ~a:
normal konvergent;
preskaŭ certe ~a:
fast
sicher konvergent, konvergent
mit der Wahrscheinlichkeit Eins;
simple ~a:
einfach konvergent, punktweise konvergent;
unuforme ~a:
gleichmäßig konvergent.
hispanaj
~i:
convergir;
~a:
convergente;
mal~i:
divergir;
unuforme ~a:
uniformemente convergente.
hungaraj
~i 2.:
egy ponton áthaladó;
~i:
konvergál, összetart, összefut;
~a:
konvergens, összetartó, összefutó;
mal~i:
divergál, széttart, szétfut;
mal~a, ne~a:
divergens, széttartó, szétfutó;
absolute ~a:
abszolút konvergens;
~a en distribuo:
elosztásban konvergens;
~a en mezuro:
majdnem mindenütt konvergens(mérték szerint) ;
~a en probablo:
sztochasztikusan konvergens;
malforte ~a:
gyengén konvergens;
norme ~a:
normában konvergens;
preskaŭ certe ~a:
majdnem mindenütt konvergens;
simple ~a:
pontonként konvergens;
unuforme ~a:
egyenletesen konvergens.
~iga:
gyűjtőlencse, konvergens lencse.
polaj
~i 1.:
być zbieżnym, zchodzić się, zbiegać się;
~i 2.:
być zbieżnym, zchodzić się, zbiegać się;
~i 4.:
być zbieżnym, zchodzić się, zbiegać się, dążyć do;
~a 2.:
zbieżny;
mal~i:
być rozbieżnym, rozchodzić się;
mal~a, ne~a:
rozbieżny;
absolute ~a:
bezwględnie zbieżny;
~a en distribuo:
zbieżny według dystrybuant;
~a en mezuro:
zbieżny według miary;
~a en probablo:
zbieżny według prawdopodobieństwa;
malforte ~a:
słabo zbieżny;
preskaŭ certe ~a:
zbieżny z prawdopodobieństwem 1;
simple ~a:
zwyczajnie
zbieżny;
unuforme ~a:
jednostajnie zbieżny.
portugalaj
~i:
convergir.
rusaj
~i 2.:
сходиться в
общей точке;
~i:
сходиться;
~a 2.:
сходящийся;
mal~i:
расходиться;
mal~a, ne~a:
расходящийся;
absolute ~a:
абсолютно
сходящийся;
~a en distribuo:
сходящаяся
по
распределению
(последовательность
случайных
переменных);
~a en mezuro:
сходящаяся
по мере
(последовательность
функций);
~a en probablo:
сходящаяся
по вероятности
(последовательность
случайных
переменных);
malforte ~a:
слабо
сходящийся;
norme ~a:
нормально
сходящийся;
preskaŭ certe ~a:
почти
наверное
сходящаяся
(последовательность
случайных
переменных), сходящаяся с
вероятностью
единица
(последовательность
случайных
переменных);
simple ~a:
поточечно
сходящаяся
(последовательность
функций), просто
сходящаяся
(последовательность
функций);
unuforme ~a:
равномерно
сходящаяся
(последовательность
функций).
fontoj
1.
Kazimierz Bein: Vortaro de Esperanto2.
Jan Werner: Matematika Vortaro, Esperanta-Ĉeĥa-Germana, „kunkura“3.
Raoul Bricard: Matematika Terminaro kaj Krestomatio, p. 174.
Raoul Bricard: Matematika Terminaro kaj Krestomatio, p. 195.
Plena Ilustrita Vortaro6.
Raoul Bricard: Matematika Terminaro kaj Krestomatio, p. 197.
Raoul Bricard: Matematika Terminaro kaj Krestomatio, p. 198.
Olav Reiersøl: Matematika kaj Stokastika Terminaro Esperanta, p. 28, sub verba formo9.
R. Hilgers: Yashovardhan: k.a.: EK-Vortaro de matematikaj terminoj, §23010.
R. Hilgers: Yashovardhan: k.a.: EK-Vortaro de matematikaj terminoj, §266, „malforta
konverĝo“11.
Raoul Bricard: Matematika Terminaro kaj Krestomatio, p. 19, p.p. serio12.
R. Hilgers: Yashovardhan: k.a.: EK-Vortaro de matematikaj terminoj, §231
[^Revo]
[konver.xml]
[redakti...]
[artikolversio:
1.40 2009/07/01 17:21:17 ]
 la sunaj radioj, trapasinte konveksan lenson,
konverĝas al ĝia fokuso [1].
la sunaj radioj, trapasinte konveksan lenson,
konverĝas al ĝia fokuso [1].
 (fakula ĵargono en geometrio)
(p.p. linioj)
Havi komunan punkton:
ĉiuj naskantoj de
konuso konverĝas
(intersekciĝas) ĉe ĝia
vertico.
(fakula ĵargono en geometrio)
(p.p. linioj)
Havi komunan punkton:
ĉiuj naskantoj de
konuso konverĝas
(intersekciĝas) ĉe ĝia
vertico.
 (elementa analitiko)
Senfina vico x1,
x2,...
konverĝas al p se por ajna pozitiva reelo
c ekzistas tia numero n, ke
|p-xi| < c
por ĉiu i > n.
(elementa analitiko)
Senfina vico x1,
x2,...
konverĝas al p se por ajna pozitiva reelo
c ekzistas tia numero n, ke
|p-xi| < c
por ĉiu i > n.
 [3]
(p.p. vico aŭ
filtrilo super
topologia spaco)
Esti konverĝa 2:
laŭdifine ĉiuj koŝiaj vicoj konverĝas
en kompleta spaco.
[3]
(p.p. vico aŭ
filtrilo super
topologia spaco)
Esti konverĝa 2:
laŭdifine ĉiuj koŝiaj vicoj konverĝas
en kompleta spaco.